ಘನಕೋನ

ಘನಕೋನ ಎಂದರೆ ಯಾವುದಾದರೂ O ಬಿಂದುವಿನಿಂದ ಒಂದು ಸೀಮಿತ ಮೇಲ್ಮೈ (ಬೌಂಡ್ ಸರ್ಫೇಸ್) S ಅನ್ನು ಅವಲೋಕಿಸಿದಾಗ ಏರ್ಪಡುವ ದೃಷ್ಟಿ ರೇಖೆಗಳ (line of sight) ಸಮಷ್ಟಿ ವಿನ್ಯಾಸ (ಸಾಲಿಡ್ ಆಂಗಲ್).^[೧]^[೨]^[೩] ದೃಷ್ಟಿರೇಖೆಗಳನ್ನು S ನಿಂದ ಆಚೆಗೂ ಅನಿರ್ದಿಷ್ಟವಾಗಿ ವಿಸ್ತರಿಸಲು ಅಡ್ಡಿಯಿಲ್ಲ. ಸೌಕರ್ಯಕ್ಕಾಗಿ O ವನ್ನು ಶೃಂಗ (apex) ಎಂದೂ, S ಅನ್ನು ಪಾದ ಎಂದೂ ನಿರ್ದೇಶಿಸುತ್ತೇವೆ. ಇಂಥ ವಿನ್ಯಾಸದ ವ್ಯಾಪ್ತಿಯನ್ನು ಅಳೆಯುವ ಸಲುವಾಗಿ O ಕೇಂದ್ರದ ಸುತ್ತ ಏಕಮಾನ ತ್ರಿಜ್ಯದ (ಯೂನಿಟ್ ರೇಡಿಯಸ್) ಗೋಳವನ್ನು ಕಾಲ್ಪನಿಕವಾಗಿ ರಚಿಸುತ್ತೇವೆ. O ನಿಂದ S ನ ವಿವಿಧ ಬಿಂದುಗಳತ್ತ ಪ್ರಸರಿಸುವ ದೃಷ್ಟಿರೇಖೆಗಳು ಈ ಗೋಳದ ಮೇಲ್ಮೈಯನ್ನು ಛೇದಿಸಿ ಅದರಲ್ಲಿ S ನ ವಿಕ್ಷೇಪ (projection) T ಯನ್ನು ಗುರುತಿಸುತ್ತವೆ. T ಯ ಮೇಲ್ಮೈ ಸಲೆಯೇ (ಸರ್ಫೇಸ್ ಏರಿಯ) ಪರಿಶೀಲಿತ ಘನಕೋನದ ಪರಿಮಾಣ.

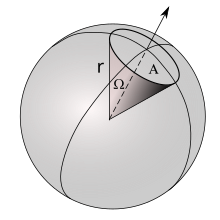
ಘನಕೋನದ ಏಕಮಾನ

ಘನಕೋನಗಳ ಅಳತೆಯ ಮೂಲಮಾನಕ್ಕೆ ಸ್ಟಿರೇಡಿಯನ್ ಎಂದು ಹೆಸರು. (stere + radian = steradians stere-|stereo- ಎಂದರೆ ಘನ ಎಂದೂ, radian ಎಂದರೆ ಕೋನವನ್ನು ಅಳತೆ ಮಾಡಲು ಬಳಸುವ ಒಂದು ಏಕಮಾನ ಎಂದೂ ಅರ್ಥ). T ಯ ಸಲೆ ಏಕಮಾನದಷ್ಟಿದ್ದರೆ S ಮೇಲ್ಮೈ O ನಲ್ಲಿ ಏರ್ಪಡಿಸುವ ಘನಕೋನ ಒಂದು ಸ್ಟಿರೇಡಿಯನ್ ಆಗಿರುತ್ತದೆ. ಏಕಮಾನ ತ್ರಿಜ್ಯದ ಒಂದು ಗೋಳದ ಮೇಲ್ಮೈ ಸಲೆ 4π x ತ್ರಿಜ್ಯದ ವರ್ಗ = 4π ಆದ ಕಾರಣ O ನ ಸುತ್ತ ವ್ಯಾಪಿಸಿರುವ ಒಟ್ಟು ಘನಕೋನ 4π ಸ್ಟಿರೇಡಿಯನ್ ಆಗುವುದು. O ಬಿಂದುವಿನಲ್ಲಿ ಈ ಸಮಗ್ರ ಘನಕೋನವನ್ನು ಏರ್ಪಡಿಸುವ ಮೇಲ್ಮೈ O ವನ್ನು ಎಲ್ಲ ದಿಶೆಗಳಲ್ಲೂ ಆವರಿಸಿಕೊಂಡು ಸಂವೃತವಾಗಿರಬೇಕಾಗುತ್ತದೆ. (ಕ್ಲೋಸ್‌ಡ್ ಸರ್ಫೇಸ್, ಉದಾಹರಣೆಗೆ O-ಕೇಂದ್ರೀಯ ಗೋಳ).

[ತಲ ಜ್ಯಾಮಿತಿಯ (ಪ್ಲೇನ್ ಜಿಯೊಮಿಟ್ರಿ) ಅನುರೂಪ ಪ್ರಕರಣದಲ್ಲಾದರೋ ಬಿಂದೊವೊಂದನ್ನು ಸುತ್ತುಗಟ್ಟುವ ಯಾವುದೇ ಸಂವೃತರೇಖೆ (ಉದಾಹರಣೆಗೆ ವೃತ್ತ) ಆ ಬಿಂದುವಿನಲ್ಲಿ ಏರ್ಪಡಿಸುವ ಸಮಗ್ರ ತಲಕೋನ (ಪ್ಲೇನ್ ಆಂಗಲ್) 2π ರೇಡಿಯನ್ ಆಗಿರುವುದನ್ನು ಹೋಲಿಕೆಗಾಗಿ ಇಲ್ಲಿ ಸ್ಮರಿಸಬಹುದು].

ಕಲನಶಾಸ್ತ್ರದ ತತ್ತ್ವಗಳ ಪ್ರಯೋಗದಿಂದ ಏಕಮಾನ ತ್ರಿಜ್ಯದ ಗೋಳಗಳ ನೆರವಿಲ್ಲದೆಯೂ ಘನಕೋನಗಳನ್ನು ಅಳತೆ ಮಾಡಲು ಸಾದ್ಯವಾಗುವುದು. dS ಸಲೆ S ಮೇಲ್ಮೈಯ ಒಂದು ವಿಕಲ ಘಟಕವಾಗಿರಲಿ (ಸರ್ಫೇಸ್ ಎಲಿಮೆಂಟ್). dS ನ್ನು O ಗೆ ಸೇರಿಸುವ ಸರಳರೇಖೆಯ ಉದ್ದ r ಹಾಗೂ ಆ ಸರಳರೇಖೆಗೂ, dS ಗೆ ಎಳೆದ ಲಂಬಕ್ಕೂ ನಡುವೆ ಇರುವ ತಲಕೋನ θ ಆದಲ್ಲಿ S ನಿಂದ O ನಲ್ಲಿ ಏರ್ಪಟ್ಟ ಘನಕೋನದ ಸ್ಟಿರೇಡಿಯನ್ ಅಳತೆ ನಿಜಕ್ಕೂ $\int \limits _{S}dS\cos \phi /r^{2}$ ಎಂಬ ಮೇಲ್ಮೈ ಅನುಕಲನಾಂಕವೇ (ಸರ್ಫೇಸ್ ಇಂಟೆಗ್ರಲ್) ಆಗುತ್ತದೆ. ಇದರಲ್ಲಿ r ಹಾಗೂ dS ಗಳ ಭೌತ ಆಯಾಮಗಳು (ಫಿಜಿಕಲ್ ಡೈಮೆನಶನ್ಸ್) ಅನುಕ್ರಮವಾಗಿ [L = ಉದ್ದ] ಹಾಗೂ [L² = (ಉದ್ದ x ಉದ್ದ)] ಆದ ಕಾರಣ dS ಮತ್ತು r² ಗಳ ಆಯಾಮಗಳು ಪರಸ್ಪರ ರದ್ದುಗೊಳ್ಳುವುವು; ಎಂತಲೇ ಭೌತಶಾಸ್ತ್ರದಲ್ಲಿ ತಲಕೋನಗಳಂತೆಯೇ ಘನಕೋನಗಳನ್ನು ಆಯಾಮರಹಿತವೆಂದು ಪರಿಗಣಿಸುವುದು ರೂಢಿ. ಘನಕೋನಗಳಿಗೆ ಎರಡು ಸರಳ ನಿದರ್ಶನಗಳೆಂದರೆ ಲಂಬವೃತ್ತೀಯ ಶಂಕು (ರೈಟ್ ಸರ್ಕ್ಯುಲರ್ ಕೋನ್) ಹಾಗೂ ಬಹುಫಲಕ ಕೋನಗಳು (ಪಾಲಿಹೆಡ್ರಲ್ ಆಂಗಲ್ಸ್).

ಲಂಬವೃತ್ತೀಯ ಶಂಕುವಿನ ಪ್ರಸಂಗದಲ್ಲಿ ಘನಕೋನದ ಪಾದ ಒಂದು ವೃತ್ತೀಯ ಫಲಕ (ಸರ್ಕ್ಯುಲರ್ ಡಿಸ್ಕ್ S). ಆ ಫಲಕದ ಕೇಂದ್ರ M ನಿಂದ ಫಲಕ ತಲಕ್ಕೆ ಎಳೆದ ಲಂಬದ ಮೇಲೆಯೇ ಘನಕೋನದ ಶೃಂಗವೂ (O) ಇರುವುದು ಅಗತ್ಯ.

ಈ ಶಂಕ್ವಾಕೃತಿಯ ಘನಕೋನದ ಪರಿಮಾಣ $4\pi \sin ^{2}{\frac {1}{2}}\theta$ ಸ್ಟಿರೇಡಿಯನ್; ಇಲ್ಲಿ θ ಶಂಕುವಿನ ಶೃಂಗಾರ್ಧ ಕೋನ (ಸೆಮಿವರ್ಟಿಕಲ್ ಆಂಗಲ್; P ಯು ಪಾದದ ಅಂಚಿನಲ್ಲಿರುವ ಯಾವುದೇ ಬಿಂದುವಾದಲ್ಲಿ ಶೃಂಗಾರ್ಧಕೋನ θ = ಕೋನ POM ಒಂದು ತಲಕೋನ ಎಂಬುದನ್ನು ಗಮನಿಸಬೇಕು).

ಬಹುಫಲಕ ಕೋನಗಳ ಪ್ರಸಂಗದಲ್ಲಿ ಘನಕೋನದ ಪಾದ ಒಂದು ಬಹುಭುಜಾಕೃತೀಯ ಫಲಕ (ಪಾಲಿಗನಲ್ ಡಿಸ್ಕ್; S ನಲ್ಲಿ ನಿದರ್ಶನಾತ್ಮಕವಾಗಿ AB, BC, CD, DA ನಾಲ್ಕು ಭುಜಗಳನ್ನು ಪ್ರದರ್ಶಿಸಲಾಗಿದೆ); ಘನಕೋನದ ಶೃಂಗ (O) ಎಲ್ಲಿ ಬೇಕಾದರೂ ಇರಬಹುದು. OAB, OBC, OCD, ODA ತ್ರಿಭುಜಗಳು ಚಿತ್ರದಲ್ಲಿ ಬಹುಫಲಕ ಕೋನದ ಫಲಕಗಳು (ಫೇಸಸ್), ಯಾವುದೇ ಒಂದು ಫಲಕದ (ಉದಾಹರಣೆಗೆ OAB) ತಲಕ್ಕೂ (ಪ್ಲೇನ್), ಅದರ ಪಕ್ಕದ ಫಲಕದ (ಉದಾಹರಣೆಗೆ OBC) ತಲಕ್ಕೂ ನಡುವೆ ಇರುವ ಕೋನಕ್ಕೆ ದ್ವಿಫಲಕ ಕೋನ (ಡೈಹೆಡ್ರಲ್ ಆಂಗಲ್, ಇದು ಒಂದು ತಲಕೋನವೇ ವಿನಾ ಘನಕೋನವಲ್ಲ) ಎಂದು ಹೆಸರು.

ಬಹುಫಲಕ ಕೋನವೊಂದಕ್ಕೆ (ಪಾಲಿಹೆಡ್ರಲ್ ಆಂಗಲ್) n ಫಲಕಗಳಿದ್ದರೆ [n = 3, 4, 5 . . . . ಚಿತ್ರದಲ್ಲಿ n = 4] ಅದು ಒಳಗೊಳ್ಳುವ ದ್ವಿಫಲಕ ಕೋನಗಳ ಸಂಖ್ಯೆಯೂ n ಆಗಿರುತ್ತದೆ. ಈ ಎಲ್ಲ ದ್ವಿಫಲಕ ಕೋನಗಳ ಮೊತ್ತ α ರೇಡಿಯನ್ ಆದಲ್ಲಿ ಬಹುಫಲಕ ಘನಕೋನದ ಸ್ಟಿರೇಡಿಯನ್ ಪರಿಮಾಣ [α - (n - 2)π] ಆಗುವುದು. ಒಂದು ಬಹುಫಲಕ ಕೋನದ ಫಲಕಗಳಲ್ಲಿ ಶೃಂಗದ ಬಳಿ ಏರ್ಪಟ್ಟಿರುವ ತಲಕೋನಗಳಿಗೆ [ಚಿತ್ರದಲ್ಲಿ AOB, BOC, COD ಹಾಗೂ DOA ಕೋನಗಳು] ಫಲಕದ ಕೋನಗಳು (ಫೇಸ್ ಆಂಗಲ್ಸ್) ಎಂದು ಹೆಸರು. ಬಹುಫಲಕ ಘನಕೋನವೊಂದರಲ್ಲಿ ಎಲ್ಲ n ದ್ವಿಫಲಕ ಕೋನಗಳೂ ಪರಸ್ಪರ ಸಮವಾಗಿರಬಹುದು; ಮತ್ತು ಎಲ್ಲ n ದ್ವಿಫಲಕ ಕೋನಗಳು ಸಹ ಪರಸ್ಪರ ಸಮವಾಗಿರಬಹುದು. ಹಾಗಿದ್ದಲ್ಲಿ ಆ ಘನಕೋನ ಒಂದು ಕ್ರಮ ಬಹುಫಲಕ ಕೋನ (ರೆಗ್ಯುಲರ್ ಪಾಲಿಹೆಡ್ರಲ್ ಆಂಗಲ್) ಎಂದೆನಿಸಿಕೊಳ್ಳುತ್ತದೆ. ಇಂಥ ಕ್ರಮ ಬಹುಫಲಕ ಘನಕೋನವನ್ನು ಸೂಕ್ತವಾದ ಒಂದು ಲಂಬವೃತ್ತೀಯ ಶಂಕುವಿನಲ್ಲಿ ಅಂತರ್ಗತಗೊಳಿಸಬಹುದು. ಆ ಸೂಕ್ತ ಪರಿಶಂಕುವಿನ (ಸರ್ಕಮ್‌ಸ್ಕ್ರೈಬಿಂಗ್ ಕೋನ್) ಶೃಂಗಾರ್ಧ ಕೋನ θ ಆದಲ್ಲಿ ಕ್ರಮ ಬಹುಫಲಕ ಕೋನದ ಸ್ಟಿರೇಡಿಯನ್ ಪರಿಮಾಣ 2[π - n arc tan (cos θtanπ/n] ಆಗುವುದು. ಒಂದೊಂದು ಫಲಕೋನವೂ f ಆಗಿರುವಂಥ ಕ್ರಮ ಬಹುಫಲಕ ಘನಕೋನದ ಪರಿಮಾಣ 2[π - n arc cos (sec 1/2f cos π/n] ಸ್ಟಿರೇಡಿಯನ್.

ಭೌತಶಾಸ್ತ್ರದಲ್ಲಿ ಘನಕೋನದ ಉಪಯೋಗಗಳು

ಹಲವಾರು ಸಂದರ್ಭಗಳಲ್ಲಿ ಘನಕೋನದ ಪರಿಕಲ್ಪನೆ ಭೌತಶಾಸ್ತ್ರಕ್ಕೆ ಉಪಯುಕ್ತವಾಗಿದೆ. ಉದಾಹರಣೆಗೆ S ಮೇಲ್ಮೈ O ಬಿಂದುವಿನಲ್ಲಿ Ω ಸ್ಟಿರೇಡಿಯನ್ ಘನಕೋನವನ್ನು ಉಂಟುಮಾಡಲಿ. ಈಗ O ಶೃಂಗ Q ಕ್ಯಾಂಡೆಲಾದಷ್ಟು ಪ್ರಕಾಶದ ಒಂದು ದೀಪ ಎಂದು ಭಾವಿಸಿದರೆ S ಮೇಲ್ಮೈ ಮೂಲಕ ಹಾದುಹೋಗುವ ದೀಪದ ಬೆಳಕಿನ ಪ್ರವಾಹದರ (ಲ್ಯೂಮಿನಸ್ ಫ್ಲಕ್ಸ್) QΩ ಲ್ಯೂಮೆನ್ ಎಂದು ವ್ಯಾಖ್ಯಿಸಲಾಗುವುದು.

ಮತ್ತೊಂದು ನಿದರ್ಶನವಾಗಿ (O ನಿಂದ ನೋಡಿದಾಗ ಅಪ್ರದಕ್ಷಿಣ ದಿಶೆಯಲ್ಲಿರುವಂತೆ) S ಮೇಲ್ಮೈಯ ಅಂಚಿನ ಉದ್ದಕ್ಕೂ C ಆಂಪೇರಿನಷ್ಟು ನಿಯತ ವಿದ್ಯುತ್ಪ್ರವಾಹವನ್ನು N ಸುತ್ತುಗಳಲ್ಲಿ ಹರಿಯಲು ವ್ಯವಸ್ಥೆ ಮಾಡಲಾಗಿದೆಯೆಂದು ಭಾವಿಸೋಣ. ತತ್ಫಲವಾಗಿ O ಬಿಂದುವಿನಲ್ಲಿ ರೂಪಗೊಳ್ಳುವ ಕಾಂತಕ್ಷೇತ್ರವನ್ನು (ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫೀಲ್ಡ್) ಆಂಪೇರ್ ಮೀಟರ್^-1 ಮಾನದಲ್ಲಿ (ಎಸ್ಐ ಪದ್ಧತಿ)

$-CN\nabla \Omega /4\pi =(-CN/4\pi )\left(i{\frac {\partial \Omega }{\partial x}}+j{\frac {\partial \Omega }{\partial y}}+k{\frac {\partial \Omega }{\partial z}}\right)$

ಎಂಬ ಸದಿಶವೂ, ಅರ್ಸ್ಟೆಡ್ ಮಾನದಲ್ಲಿ (CGS ಪದ್ಧತಿ) ( $-CN\nabla \Omega /10$ ) ಎಂಬ ಸದಿಶವೂ ವ್ಯಕ್ತಪಡಿಸುತ್ತವೆ. ಇಲ್ಲಿ ಲಾಂಬಿಕ ಕಾರ್ಟೀಶಿಯನ್ ನಿರ್ದೇಶಕ x,y,z ಗಳನ್ನು SI ಪದ್ಧತಿಯಲ್ಲಿ ಮೀಟರುಗಳಲ್ಲೂ, CGS ಪದ್ಧತಿಯಲ್ಲಿ ಸೆಂಟಿಮೀಟರುಗಳಲ್ಲೂ ಅಳೆಯಬೇಕು. i, j, k ಇವು x, y, z ಅಕ್ಷಗಳ (axes) ನೇರದಲ್ಲಿನ ಏಕಮಾನ ಸದಿಶಗಳು.

ಉಲ್ಲೇಖಗಳು

↑ Solid angle. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Solid_angle&oldid=31702
↑ https://spie.org/publications/spie-publication-resources/optipedia-free-optics-information/fg11_p02_solid_angle
↑ https://www.mathsisfun.com/definitions/solid-angle.html

ಹೊರಗಿನ ಕೊಂಡಿಗಳು

Arthur P. Norton, A Star Atlas, Gall and Inglis, Edinburgh, 1969.
M. G. Kendall, A Course in the Geometry of N Dimensions, No. 8 of Griffin's Statistical Monographs & Courses, ed. M. G. Kendall, Charles Griffin & Co. Ltd, London, 1961
Weisstein, Eric W., "Solid Angle", MathWorld.

[1] Solid angle. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Solid_angle&oldid=31702

[2] ttps://spie.org/publications/spie-publication-resources/optipedia-free-optics-information/fg11_p02_solid_angle

[3] ttps://www.mathsisfun.com/definitions/solid-angle.html

[೧]

[೨]

[೩]